Cyts
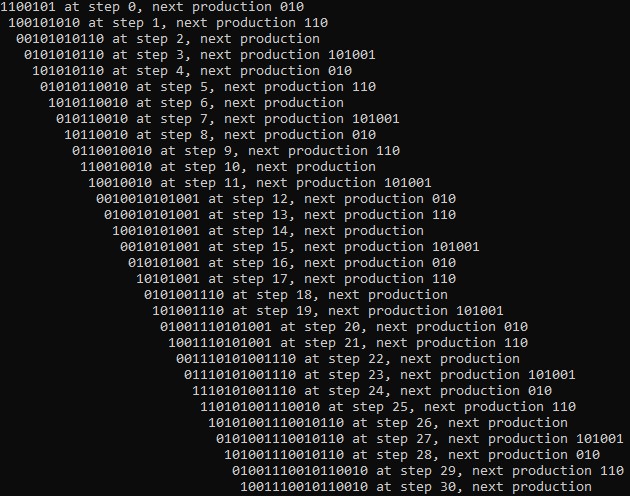
Table of Contents
Introduction #
Cyclic tag systems are a very simple Turing-complete computational model and can be thought of as very abstract computers. Cyts is a fully-featured interpreter for cyclic tag systems written in Haskell. Cyts can simulate a user-supplied cyclic tag system, taken through an interactive CLI or from a command-line flag, and pretty-print the output like in the header image. Cyts runs the given system out to an adjustable number of steps given by the -n flag.
Additionally, Cyts can detect whether the cyclic tag system halts in the given runtime and at what step. Cyclic tag systems halt in two ways: either the register clears, which is trivial to detect, or the system enters a state loop, which requires a quadratic search of the list of states of the machine. Cyts recognizes both kinds of halts and will search for them if the -r flag is given.
Development process #
I built Cyts initially as a small project to practice Haskell development and mess with an interesting example of a very simple Turing-complete system, and wrote about the process here. Afterwards, I decided to add some form of user input, which snowballed into building a full CLI and converting Cyts from a small script into a full Cabal project. I plan to cover its development in a series of blog posts.
Cyts’ scripting mode was motivated by my realization that it was perfect to use as a data generation tool. To see how, consider how a certain cyclic tag system is represented. Cyclic tag systems are specified by lists of finite binary strings:
$$ \underset{start}{001}, \space \underset{prod1}{101}, \space \underset{prod2}{110}, \space \underset{prod3}{01} $$
The first element is the starting word, and everything after is the list of productions given in order. We can map finite binary strings one-to-one to integers \(n \geq 1\) by appending a 1 to the leftmost side and then taking the (unsigned integer) base 10 representation.
$$ 00101 \mapsto \underline{1}00101 \mapsto 37 $$
This lets us convert our specification into a vector with \(p+1\) columns, where \(p\) is the number of productions:
$$ 001, 101, 110, 01 \mapsto \begin{pmatrix} 11 & 15 & 16 & 5 \end{pmatrix}$$
Cyts can recognize at what step the cyclic tag system halts, so we can label each vector in \(p+1\)-dimensional space with the step the associated system halted at, or -1 if it didn’t halt. I wrote a shell script to collect this data into a CSV, generating a few datasets which can be found here. Each dataset has \(p+1\) features, those being the starting word and \(p\) productions, and one response variable halt output from Cyts.
Data-driven cyclic tag system analysis #
There’s a good reason to generate all this data. Each dataset contains all cyclic tag systems that have \(p\) productions and starting word/productions capped at a maximum length.1 We can use this data to find heuristics that tell us whether a cyclic tag system might halt before a fixed number of steps, which I plan to use machine learning to do. This isn’t solving the halting problem (which is uncomputable), but a weaker computable version: solving whether a program halts before a fixed number of steps.
I’ll be considering the classification version of this problem, which is thresholded halt: 1 if it’s nonnegative (denoting a halted cyclic tag system,) and -1 if it’s negative (which agrees with the raw data as denoting an unhalted cyclic tag system). The data’s in a form that lends itself well to neural networks2, and so I plan to train two neural networks: a feed-forward neural network, and a convolutional neural network that seeks to incorporate positional information in the binary strings. Stay tuned for updates!
In each output CSV, the second number in the filename is \(2^l - 1\) where \(l\) is the maximum length of any word or production in that CSV. ↩︎
While I’ll experiment with other models as well, I expect worse results. This is because the conversion that takes binary strings to integers doesn’t match up well with edit distance; for example, 011 and 100 map to 11 and 12 which are as close as possible even though the edit distance between the two binary strings is as large as possible. ↩︎